1) ROTAZIONE DELL’ATTREZZATURA ATTORNO AD UN PUNTO.
In 1) abbiamo la condizione di partenza.
Il punto <A> del soggetto finisce sul punto <a> del sensore.
<F> è la lunghezza focale.
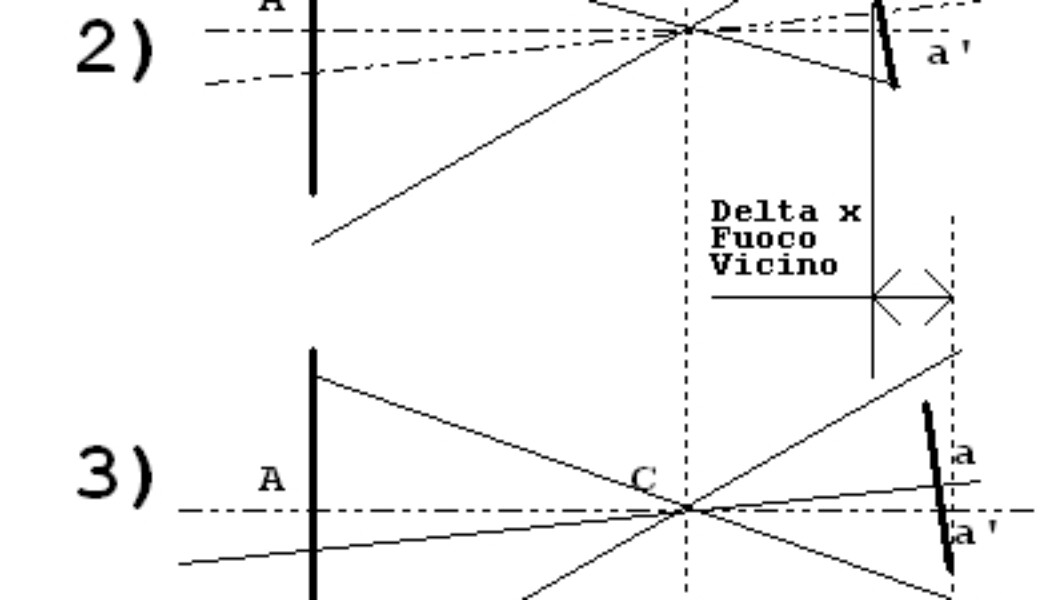
In 2) abbiamo la rotazione più semplice. Quella attorno al punto di prospettiva.
Più semplice è riferito sia al calcolo del mosso, sia al servomeccanismo.
Infatti quando tutto il servomeccanismo è contenuto nell’obiettivo non serve nessun calcolo.
È sufficiente che si opponga al moto.
Con questa rotazione il punto <A> va a finire sul punto <a’>.
La distanza tra i due è il diametro del cerchio di confisione.
In 3) abbiamo spostato il sensore, rispetto al punto di prospettiva, con un tubo di prolunga (+ messa a fuoco).
In 4) abbiamo una situazione un pò più realistica.
Il punto di rotazione è al centro delle mani che qui è fatto coincidere con il centro del sensore.
Il punto <A> ora va a finire sul punto <a”> diverso da <a> e da <a’>.
Esaminiamo la fig. 2) il caso più semplice.
[01] d = Distanza tra a e a’ = Diametro del circolo di confusione.
[02] x = Angolo di rotazione (in radianti ed inversamente proporzionale al tempo)
[03] d = x * F
Secondo la [03] il diametro del circolo di confusione dipende solo dalla lunghezza focale <F>.
Inoltre la [03] (composta solo da <x> e <F>) può essere estesa a focali qualsivoglia piccole, confermando i Post.
Però c’è un qualche però.
1a) Come abbiamo visto nella descrizione a causa dello specchio <F> non può essere piccolo a piacere.
In una macchina a telemetro, un obiettivo da 10mm può avere la pupilla d’uscita a 10mm dal sensore e con una BFD ancora minore.
In una reflex questo NON è possibile.
Semplicemente perché lo specchio non ci sta (quando lo elimineranno né riparleremo).
Se ipotizziamo un <F> minimo attorno ai 40-50mm (un pò meno per gli EF-S) non commettiamo un grosso errore.
1b) La figura 3) illustra un tubo di prolunga la cui lunghezza si somma ad <F>.
(La variazione di <F> nella messa a fuoco su soggetti vicini vedi fig.4 si somma anche lei).
Se usiamo un 50mm con 50mm di tubi di prolunga per avere un rapporto 1:1 il tempo diventerà almeno 1/100.
1c) I formati più piccoli si devono ingrandire di più.
Il diametro del circolo di confusione deve essere quindi più piccolo.
In pratica per l’APS-C occorre diminuire il tempo di 1.6 volte (1/80 invece di 1/50).
In alternativa si può usare la famigerata Focale Equivalente, il che è la stessa cosa.
Nota: vale anche per i duplicatori.
Il caso 2) però è un caso semplice, ma non realistico.
Nei casi pratici l’obiettivo non ruoterà attorno al punto di prospettiva, che non sappiamo neppure dove è messo, ma attorno al punto dove impugniamo la fotocamera.
Per i tele usiamo due mani una sul corpo ed una sull’ottica e forse non siamo distantissimi da questo esempio.
Per gli obiettivi piccoli però normalmente impugniamo il corpo macchina.
In questo caso la rotazione avviene vicino al sensore e l’effetto è maggiore perché si sposta anche il punto di prospettiva.
Ho duplicato, ingrandita, la fig. 4 così si vedono meglio i parametri coinvolti.
Il punto di prospettiva si sposta di:
[04] e = F * x
[05] d = F * x * ((D + F) / D)
La differenza è consistente nella macro dove <D> ed <F> sono cofrontabili.
Al rapporto 1:1 dobbiamo dimezzare il tempo fornito dalla [03] quindi 1/200 invece di 1/100.
Dalla descrizione Canon sembrerebbe che neppure il nuovo stabilizzatore del 100 macro IS tenga conto di questo.
Per considerare la posizione del centro di rotazione, lo stabilizzatore dovrebbe avere, infatti, due coppie di sensori una in cima ed una in fondo all’obiettivo.
Invece per distanze grandi rispetto alla focale la [05] equivale alla [03].
A D = 10F (0.5m con il 50mm) la differenza è solo del 10%.
Questo ci tranquillizza sul buon funzionamento degli attuali stabilizzatori.
2) SPOSTAMENTO LINEARE SUL PIANO DEL SENSORE.
È la nuova stabilizzazione introdotta nel 100 Macro IS.
Spostando linearmente il sensore di una quantità <e> abbiamo che il punto di prospettiva si sposta in <C’>.
Il pixel su cui finiva il punto <A> si è spostato anche lui di <e> ed ora si trova in <a’>.
L’immagine di <A> passando dal nuovo punto di prospettiva <C’> non cade in <a’>, ma in <a”>.
La distanza <d> tra <a’> e <a”> è il diametro del cerchio di confusione anche in questo caso.
La geometria è simile a quella appena vista:
[06] d = e * ((D + F) / D) – 1)
Nella macro con rapporto 1:1 il diametro del cerchio di confusione è quindi pari allo spostamento.
A distanze normali invece l’errore è irrilevante.
Ad una distanza di 10 volte la lunghezza focale è 1/10 (circa) e si riduce a zero sui panorami.
Diversi canoniani attendevano frementi il nuovo sistema applicato a tutti gli stabilizzati e chiedevano ansiosamente:
“Quando? Quando? Quando? Arf! Arf! Quando? Quando? Quando? ……”
Vista questa geometria, penso che la loro attesa sarà delusa, almeno per un pò (180 Macro a parte).