Su molti messaggi, come regola per non avere foto mosse, è “acriticamente” indicato di usare un tempo:
T(in secondi) = 1/Focale(in mm)
Esempi:
Con una focale di 100mm si dovrebbe usare un tempo di 1/100″ od inferiore.
Con una focale di 400mm si dovrebbe usare un tempo di 1/400″ od inferiore.
La regola, ora la si chiamerebbe equazione, non è nuova.
È una delle vecchie regole empiriche, ma funzionali, ideate per ridurre gli errori in tempi che erano privi di strumenti.
Tipo, ad esempio, la dimenticata regola del 16 (nota 1 a fine testo) per l’esposizione.
Questa regola era stata stata ideata per evitare il mosso quando si usavano i teleobiettivi.
In pratica, nel formato 35mm e con l’obiettivo standard di 50mm per avere una foto nitida occorreva 1/50″.
Raddoppiando la focale, si raddoppiavano anche le vibrazioni, ed era necessario dimezzare il tempo.
Usare il tempo di “1/F” forniva un buon risultato senza bisogno di calcoli complessi
Ho evidenziato “acriticamente” perché questa regola è molto spesso, anzi direi quasi sempre, applicata a qualsiasi focale senza mai chiedersi se si può fare.
Ad esempio in un post recente (non so se sia l’ultimo in ordine di tempo)
[url]forum_forum.asp?forum=6§ion=9&post=362709[/url]
per una focale di 10mm (su APS-C) si afferma che 1/5 di secondo è un tempo di sicurezza.
Sarà vero che quest’estensione a focali molto piccole è sempre valida?
Gli esperimenti mentali non costano nulla.
Proviamo a farne uno.
Estendiamo questo ragionamento a focali più corte di 10mm.
Usando un tubo di prolunga che porta il tiraggio a 160mm possiamo montare sulla reflex l’obiettivo di un microscopio.
Alcuni obiettivi ad immersione possono arrivare ad una focale di quasi 1mm con rapporto di riproduzione superiore a 100:1.
Con questo equipaggiamento possiamo fotografare un batterio.
La regola afferma che possiamo ottenere una foto nitida fotografando a mano libera, ed usando un tempo superiore ad un secondo.
Penso che questo sia considerato assurdo da tutti.
Non credo esista qualcuno che lo consideri realistico.
Dovrebbe quindi essere evidente a tutti che noi non possiamo estendere questa regola al di fuori del suo campo d’applicazione.
Ho cercato in rete dei disegni sulla geometria del mosso, ma non né ho trovato alcuno.
Probabilmente i Guru di Internet ritengono inutile fare una cosa complicata, e che fornisce risultati aleatori, quando ognuno, con 4 o 5 fotografie, si ricava i tempi reali di cui avrà bisogno per tutta la vita.
Dal mio punto di vista, se la motivazione è questa, hanno ragione da vendere.
Non credo che neppure gli iscritti al Forum più pignoli, e/o integralisti, arrivino ad affermare che, per avere una foto nitida, con un obiettivo da 100mm devo usare 1/100 mentre con uno da 101mm devo portare il tempo ad 1/101 altrimenti viene mossa.
Tuttavia questa cosa ogni tanto origina discussioni lunghe e prolisse.
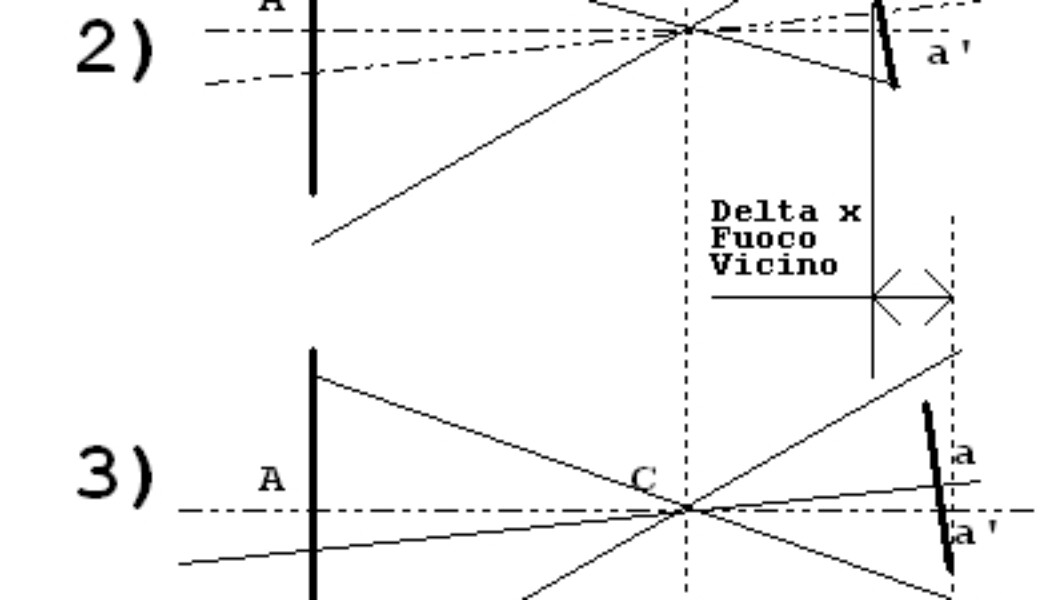
Metto perciò qualche disegno per chiarire alcune cose che, mi sembra, non siano chiare a tutti.
Le parole spesso sono oscure, ma i disegni in genere sono recepiti assai meglio.
Mi scuso per la cattiva qualità dei disegni ma sono fatti con un CAD elettrico.
Descrizione dell’origine del mosso.
Le mani che impugnano la fotocamera non sono una morsa.
Si muovono, per alcuni poco per altri tanto, su tre assi lineari ed altrettanti di rotazione.
Per di più, il movimento delle due mani non è identico.
Il movimento risultante della fotocamera è naturalmente complesso, piccolo, ma complesso.
Per i nostri fini però si può separarlo nelle sue componenti elementari analizzandole separatamente.
Tralascio la somma dei risultati parziali.
Mi limito a segnalare che la somma NON è algebrica.
I movimenti elementari, nei quali si può decomporre quello totale, sono:
1) Rotazione dell’attrezzatura attorno ad un punto. Due assi.
Quello che in lingua anglosassone si chiama Tilt.
2) Spostamento lineare sul piano del sensore. Due assi.
Quello che in lingua anglosassone si chiama Shift.
3) Rotazione sull’asse ottico. Un asse.
È il risultato di movimenti lineari differenti sui lati del sensore.
i.e. Le due mani non si muovono in modo perfettamente identico (opure c’è né usa una sola).
Non conosco il termine anglosassone.
4) Spostamento lineare sull’asse ottico. Un asse.
Non conosco il termine anglosassone.
Penso Axial Shift visto che Focus Shift indica un’altra cosa.
Prima di procedere, una notazione molto importante.
Ho scelto la chiarezza (che mi sembra importante) a scapito della precisione (che qui mi sembra inutile).
Nel testo ho, quindi, effettuato molte approssimazioni ignorando tutti quei parametri che complicavano le cose senza apportare valori significativi.
Quattro approssimazioni in particolare.
a) In tutti i luoghi dove questo era possibile, l’obiettivo è stato assimilato ad una lente sottile.
Dove non era possibile lo ho evidenziato.
b) Dati i piccoli angoli ho usato ovunque questa uguaglianza:
Tan(x) = Sin(x) = x (x in radianti)
c) Per il medesimo motivo del punto b) le distanze sul sensore sono sempre considerate con il sensore perpendicolare all’asse ottico, o parallelo al soggetto.
Anche dove è inclinato.
Tra le due ipotesi ho usato quella più conveniente.
d) Con <F> è indicata la lunghezza focale.
In realtà questa è la distanza posteriore ricavata dall’equazione coniugata delle lenti.
Distanza cui devono essere aggiunti eventuali tubi di prolunga.
F è uguale alla focale solo con soggetti all’infinito, e senza tubi di prolunga.
Normalmente il valore è maggiore del valore focale.