2.0 Errori frequenti e Atipicità.
Mettere a fuoco rapidamente, e in modo preciso, un soggetto qualsiasi, con un’illuminazione qualsiasi e con un’ambientazione qualsiasi non è un’operazione facile. In materia, il nostro occhio, pur non essendo perfetto, ha eccellenti prestazioni, ma dietro di se ha tre miliardi d’anni di evoluzione.
Non sono bruscolini!
Richard Dawkins dice che l’evoluzione è cieca (sic) e agisce a caso, può darsi che per l’evoluzione abbia ragione, ma la selezione naturale è fortemente meritocratica. Chi non metteva a fuoco, bene e rapidamente, un leone era assoggettato a una punizione che oggi riteniamo inaccettabile anche per i reati più gravi. Ciò ha fatto si che l’occhio abbia raggiunto prestazioni eccezionali. Prestazioni che l’Autofocus delle fotocamere non ha, non ancora, raggiunto.
È, perciò, plausibile che in situazioni insolite, o in condizioni difficili, fallisca e commetta degli errori, ma stranamente, le proteste di malfunzionamento che si leggono sul Web, non riguardano mai questi casi che, per un eufemismo, chiamo poco frequenti, ma dovrei chiamare rari.
Riguardano, invece, scenari del tutto normali, privi di qualsiasi elemento insolito, dove l’automatismo dovrebbe funzionare correttamente.
Queste lamentele sono diversificate ma, in genere, hanno un elemento in comune:
“Non sono quasi mai sufficientemente documentate da poter stilare un giudizio affidabile”.
Le poche volte che nelle denuncie di malfunzionamento la prova è documentata abbastanza bene da poter stilare un giudizio, si rintracciano degli errori di esecuzione che fanno addebitare il malfunzionamento al fotografo e non al meccanismo.
Direte: “Ma l’autofocus non fa tutto da solo?” Certo! E compensa pure alcuni errori del fotografo, ma non tutti gli errori del fotografo.
Anche lui ha dei limiti, come il picchio di Omar Simpson, quando era il responsabile della sicurezza in una centrale nucleare. Anche se ci riteniamo superiori a queste cose, per utilizzarlo bene dobbiamo imparare come funziona, magari non in dettaglio, ma conoscere i suoi limiti è necessario.
Nei capitoli seguenti, 2.1, 2.2 e 2.3, ho inserito gli errori più frequenti che s’incontrano sul Web.
Nel § 2.4 ho inserito due situazioni atipiche che ho incontrato durante queste prove e nei capitoli § 3… una descrizione molto succinta di come funziona.
2.1 Errori frequenti.
Ritenere che il fuoco cada a metà tra le due zone sfocate.
Questo è valido solo per le distanze della macrofotografia.
Aumentando la distanza, le due zone diventano sempre più asimmetriche fino a quando, raggiunta l’Iperfocale, la zona lontana schizza all’infinito.
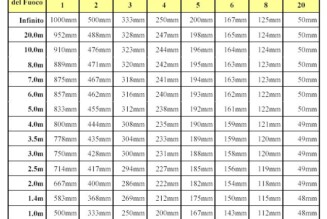
Questo è un grafico d’esempio che copre la distanza da 250 mm a 10 m. Distanze usuali per un Test casalingo dell’Autofocus.
È un grafico ricavato con Excel. In attesa di poter allegare il file, inserisco le formule così ognuno si può costruire il grafico del proprio obiettivo, nelle sue condizioni.
Profondità di campo vicina (Near) = u –{(u*f*f – N*c*f*(1/p – 1)*(u-f)) / (f*f + N*c*(u-f))}; [2.1.1]
Profondità di campo lontana (Far ) = {(u*f*f + N*c*f*(1/p – 1)*(u-f)) / (f*f – N*c*(u-f))} – u; [2.1.2]
Dove: c = Diametro del circolo di confusione (30 μm per il 24×36; 20 μm per l’APSc)
f = Lunghezza focale dell’obiettivo
N = Diaframma (1,4; 1,8; 2; … )
p = Guadagno pupillare (Diametro Pupilla d’Uscita / Diametro Pupilla d’Ingresso)
u = Distanza del Punto a Fuoco (del soggetto naturalmente)
Chiaramente le misure spaziali devono essere espresse nella medesima Unità (mm o cm o m).
Queste due formule sono molto semplici e questo, data la complessità di un obiettivo, indica subito che sono state fatte numerose approssimazioni (nota 2.1.1), alcune trascurabili, altre meno.
Elenco delle principali approssimazioni:
1°. La formula prevede una messa a fuoco fatta muovendo tutto il barilotto.
Quello che nella Terminologia inglese è chiamato Unit Focusing.
Questa è un’approssimazione che, con i moderni obiettivi Autofocus, di solito non è per niente trascurabile, ma è, invece,molto importante (nota 2.1.3).
2°. Non considera la diffrazione.
A diaframmi chiusi e rapporti d’ingrandimento alti la diffrazione è importante (nota 2.1.2).
3°. I raggi sono considerati parassiali.
Per la profondità di campo è un’approssimazione trascurabile. Ha effetti rilevabili solo per soggetti molto vicini (macro) o ai bordi di grandangolari spinti.
4°. Non è considerato il Blurr causato dalle aberrazioni dell’obiettivo (e naturalmente nemmeno quello causato dai movimenti della fotocamera). Potrebbe non essere trascurabile ma non entra mai nelle formule perché è sconosciuto. Chi ha un’idea del suo valore può diminuire adeguatamente il diametro del circolo di confusione (nota 2.1.2).
5°. Il diaframma è considerato perfettamente circolare.
L’effetto della non circolarità, per quanto riguarda gli obiettivi attuali, però, è irrilevante.
I catadiottrici, infatti, nonostante la loro forma sia una corona circolare, hanno una profondità di campo simile a quella degli obiettivi a lenti, e diaframmi a saracinesca, come quelli delle fotocamere usa e getta di anni fa, non se né vedono più in giro.
6°. Altri parametri minori.
Nota 2.1.1).
Le approssimazioni introdotte in [2.1.1] e [2.1.2] sono usate dappertutto, anche nei calcolatori della profondità di campo disponibili On Line. Anzi la maggioranza di questi non considera nemmeno il guadagno pupillare e lo approssima a 1.
Nota 2.1.2).
Gli effetti dei vari Blurr (termine ormai entrato anche nell’italiano dei fotoamatori) non si sommano in modo semplice e non si possono inserire nell’equazione della profondità di campo con una semplice somma. Tuttavia è abituale, anche se non è esatto, considerare che il diametro totale del circolo di confusione sia dato da:
Radice Quadrata ( CDOF
2 + CDIFF
2 + COB
2 + CMOSSO
2 + …)
Conoscendo, anche se in modo approssimato, i vari valori si può eseguire il calcolo inverso e trovare il valore del circolo di confusione da inserire nella formula.
Il diametro del circolo di confusione dato dalla diffrazione è universalmente considerato il diametro del primo circolo di Airy:
CDIFF = 2,44*λ*N*(1+m)
Dove:
λ È la lunghezza d’onda della luce che va da 0,4 a 0,7 m è dovrebbe esse fissata a 0,7 um (rosso) ma normalmente è messa a 0,546 um (giallo-verde).
m È il rapporto di riproduzione. In macrofotografia, e soprattutto in microscopia, diventa importante ma nella fotografia normale è molto piccolo e può essere lasciato a zero.
Qui una tabellina con il diametro del primo circolo di Airy in um, da confrontare con il diametro del circolo di confusione che vale 30 um per il 35 mm e 20 um per l’APS-C.
Nota 2.1.3).
Negli obiettivi Autofocus il sistema di muovere tutto l’obiettivo non è più usato perché dovendo muovere masse elevate per lunghe distanze, è lento. Adesso quasi tutti gli obiettivi autofocus hanno la messa a fuoco interna. Con questi sistemi (né esistono diversi) durante la messa a fuoco cambiano diversi parametri, in primis la lunghezza focale. Non conoscendo né cosa cambia, né come, la profondità di campo in funzione della distanza, di questi obiettivi non è completamente predibile, e occorre misurare, almeno l’effettiva lunghezza focale a quella distanza e le posizioni delle due pupille, perché le differenze tra un tipo di obiettivo e l’altro possono essere rilevanti.
Punti a profondità diverse nell’area inquadrata dall’Autofocus.
Sono presenti nella stragrande maggioranza delle immagini allegate alle dichiarazioni di malfunzionamento.
Questo è un errore gravissimo.
Il motivo è molto semplice ed è illustrato in dettaglio nel capitolo 3.5.
L’Autofocus della fotocamera inquadra una certa area e agisce sulla messa a fuoco in base alle informazioni che ricava da tutta l’area, mediante algoritmi che non conosciamo. Quando nell’area sono, inclusi punti posti a distanze diverse, non sappiamo dove la macchina mette a fuoco. Qualcuno parla di punto intermedio ma, non conoscendo gli algoritmi della fotocamera, non possiamo dire nulla. Il punto in cui la fotocamera mette a fuoco, in casi come questi, è semplicemente sconosciuto. Sicuramente è da qualche parte tra il punto più vicino e quello più lontano, ma non è noto dove.
Dite che nelle fotografie reali l’area inquadrata dall’Autofocus contiene sempre punti a distanze diverse?
OK! È vero, ma spetta a noi saperlo e sfruttare adeguatamente la profondità di campo, e, dove le contromisure non fossero adeguate, ricorrere al sempre presente fuoco manuale. L’automatismo non (non ancora) ci sostituisce completamente negli scatti. Quando facciamo il Test, invece, dobbiamo proprio misurare il comportamento dell’automatismo e lo dobbiamo fare in modo affidabile, ripetibile ed esportabile. Ora, per ottenere un risultato ripetibile ed esportabile, è assolutamente necessario avere l’area del soggetto inquadrata dal sensore dell’Autofocus situata tutta su di un unico piano ortogonale all’asse ottico (o aggiungere tutte le misure necessarie per la valutazione).
Non considerare che l’Autofocus è tarato con un po’ di Front Focus.
Argomento trattato nel capitolo 3.4.
Target non ortogonale all’asse ottico.
Già detto, ma non fa male ripeterlo “Sensore e Target devono essere paralleli”. Il parallelismo non è così critico come nelle misure di risoluzione, ma è bene rispettarlo meglio che si può.
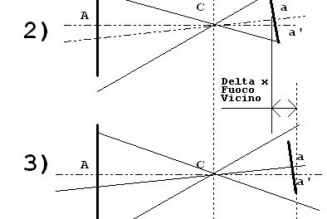
Quando non è rispettato (vedi Figura 2.1.2), dimensioni e distanze dal piano focale cambiano e questo introduce un’incertezza nel valutare il punto esatto dove cade il fuoco.
Nota: la scala inclinata è inclinata su un solo asse. L’altro deve essere ortogonale!
Per un controllo, si può verificare l’immagine su tutti i lati del Target.
Devono essere identici in fuoco e fattore di riproduzione. Se non lo sono, significa che o non è parallelo, o è decentrato, o entrambi.
Misurare le distanze dei due lati con un metro è sufficiente per la precisione richiesta, ma i più pignoli possono ricorrere a due scelte.
Bolle.
Con una bolla si riducono i tempi di allineamento camera – immagine.
L’economico oggetto a sinistra, che non so da chi sia costruito, ma è commercializzato da Manfrotto, nonostante sia un coso di plastica stampata, ha una precisione eccellente. Quello più costoso a destra, ha il vantaggio di fornire l’angolo e consente di misurare alcune cose in più.
Aiuto per il Parallelismo.
I pignolissimi, che amano il bricolage, possono sfruttare le proprietà dei triangoli isosceli costruendosi quest’oggetto.
In un qualsiasi Brico Center si acquistano tre stecche di legno. Sulla base si praticano tre fori, due ai lati per connettere i cateti e uno al centro per inserire la mira. Sui due catet la distanza, naturalmente dopo averli sovrapposti per avere sempre i lati identici. In questo modo, tenendo la mira al centro del mirino, abbiamo un parallelismo entro qualche frazione di grado. È utilizzabile sia orizzontale sia in verticale.
È un oggetto utile per provare la risoluzione degli obiettivi, dove le richieste di parallelismo sono stringenti.
Per provare solo l’Autofocus non è necessario ma, poiché le operazioni ripetitive sono numerose, può darsi che, nelle prove, faccia risparmiare più tempo di quello speso a costruirlo.
Blocco gambe cavalletto.
Continuando a gironzolare attorno al cavalletto per le numerose manovre ripetitive è facile urtalo. Spostarlo, anche di poco, significa ricominciare il lavoro da capo.
Si può evitare facendo, con due stecche di legno, quest’appoggio. Il diametro dei pozzetti dipende dalle dimensioni dei piedini del treppiede.
Naturalmente non è appoggiato al suolo direttamente, ma con tre piedini per mobili, altrimenti balla.
Sul supporto si mettono tre secchi pieni d’acqua. Uno da 20 litri sul braccio più lungo e due da 10 litri sui due più bracci corti.
Fatto questo, il cavalletto è una roccia. Rimane al suo posto per (quasi) ogni urto e se per caso i piedini saltano fuori dai pozzetti rimettendoli dentro conservano la medesima posizione di prima.
2.2 Cose da non trascurare.
Ci sono poi alcune cose che non sono dei veri errori, ma non andrebbero trascurate.
Le macchine fotografiche sono progettate per scattare fotografie, non per
funzionare da strumenti di misura.
Le loro prestazioni sono calibrate su quelle delle ottiche. La risoluzione, ad esempio, è quella di un buon obiettivo o poco superiore. Nell’uso come strumento di misura una risoluzione di 10 volte quella dell’obiettivo (800 linee/mm, 19200×28800=553MPixel) sarebbe utile ma usandola per scattare foto è, invece, nociva. La risoluzione della foto, infatti, non migliora perché è limitata dall’obiettivo, mentre peggiorano di 100 volte (vanno con il quadrato) il rumore e la dimensione dei file.
È, quindi, del tutto normale trovare una certa variabilità nelle misure, nonché qualche difficoltà, o impossibilità, a realizzarne alcune con sufficiente precisione.
Questo vale anche per i siti Internet che usano una fotocamera per le misure! Non bisogna prestare una fede religiosa a certi parametri dati con molti decimali.
Purtroppo, per verificare l’autofocus di una fotocamera è inevitabile usare la medesima fotocamera. Una variabilità di un 5% ÷ 10%, per questo Test casalingo è, quindi, nella norma.
Farci sempre venire dei dubbi, specialmente un paio:
– “Che cosa succede se … ?”
– “Sono sicuro che le mie opinioni, e le condizioni di contorno, non influenzino la misura?”
I Test, sovente, sono considerati dotati di esistenza propria (concetto Platonico), ma questo è vero solo per le procedure standardizzate e solo entro i loro limiti.
Non è, invece, vero per i Test non standard, qualsiasi essi siano. Questi Test sono influenzati non solo dal modo in cui sono fatti (principalmente) e dall’ambiente in cui sono svolti ma anche dalle nostre opinioni e/o modo di pensare. Quando noi facciamo qualcosa, quello che facciamo, e come lo facciamo, dipende sempre
dalla nostra personalità. Dobbiamo, perciò, tenere bene in mente che commettiamo sempre qualche errore. Molti di questi errori sono del tutto trascurabili e spesso sono pure inevitabili perché eliminarli, totalmente, può rendere impossibile l’esecuzione del Test, ma questo non è vero per tutti.
Alcuni possono essere importanti e non evidenti immediatamente, ma solo dopo lungo cogitare. Per ridurli, esaminiamo molto criticamente il nostro lavoro, qualsiasi cosa facciamo. Le cantonate si prendono lo stesso ma, se si è autocritici, se né prendono di meno.
Gli effetti della prospettiva.
Usando la scala inclinata, la prospettiva va vista sotto i due aspetti del Target e della Scala Inclinata.
Target
Nella configurazione standard il Target è perpendicolare all’asse ottico.
Anche la linea nera della Focus Test Chart di Tim Jackson può essere considerata ortogonale, perché è sottile e la differenza tra i due bordi è irrilevante.
Con un’immagine ortogonale all’asse ottico, non esistono problemi prospettici. Con un soggetto tridimensionale o inclinato, invece, la prospettiva può avere un po’ d’importanza nella valutazione visiva. Qui un esempio con linee e sfere riprese con un obiettivo da 120 gradi.
Le linee sono riprodotte in modo fedele indipendentemente dalla distanza dall’asse ottico, le sfere, invece, sono trasformate in ellissoidi con l’asse sul piano del sensore maggiorato. Usualmente non abbiamo una prospettiva così estrema, ma non trascuriamola lo stesso e, quando esaminiamo l’immagine, teniamola
presente.
Scala Inclinata.
Nella configurazione standard, la scala è inclinata di 45° (o 30°, o 60°) e la prospettiva influenza ciò che vediamo in maniera consistente.
Ecco due immagini d’esempio.
Focale . . . = 50 mm Focale . . . = 100 mm
Distanza . . = 50 cm Distanza . . = 100 cm
Rapporto di riproduzione = 1:9,86 Rapporto di riproduzione = 1:10
Diaframma . . = 1:2,8 Diaframma . . = 1:2,8
Inclinazione . . = 45° Inclinazione . . = 45°
La profondità di campo è quasi identica, perché quasi identico è il rapporto di riproduzione (1:10).
Cambia solo il punto di prospettiva, 0,5 m la prima immagine, 1,0 m la seconda.
Eccole le immagini:
Se ci limitiamo all’aspetto visivo, questo è molto diverso. Guardando, invece, il grafico del contrasto:
L’andamento è simile, il punto di miglior fuoco s’identifica abbastanza bene in entrambi i casi, e si vede anche come la variazione della densità di linee/mm sul sensore modifichi la zona della profondità di campo.
La scala inclinata è, quindi, buona e valida, ma deve essere controllata senza farsi ingannare dalla prospettiva e non trascurando la diversa risoluzione tra il lato vicino e quello lontano.
2.3 Cose da non fare
Taroccare le foto.
Aumentare contrasto e nitidezza per migliorare il contrasto dei grafici.
Non va bene poiché per testare l’Autofocus usiamo proprio questi due parametri.
Aumentare il contrasto non è grave. Ho provato, con la scala A1_SIR_10, a confrontare i profili di una linea a fuoco e di una linea sfocata, tra l’immagine originale e una ottenuta spostando al massimo i cursori di luce e ombre su DPP. Questi sono i grafici adattati al medesimo contrasto.
Sono molto simili, sia la parte a fuoco sia quella sfocata (_Sf) quindi, non dovrebbero causare errori.
Non sono però identici nella parte mediana, quindi, non essendo la modifica necessaria, meglio non toccare nulla.
2.4 Funzionamenti atipici.
Durante le prove per questo testo, ho incocciato in due funzionamenti per me non usuali.
Ho sottolineato il per me poiché non mi attendevo questo comportamento ma ritengo abbiano una spiegazione logica.
Primo Caso particolare.
Luce . . . . . . . 12 EV
Diaframma . . . . . . F/2,8
Focale (100 Macro Canon), . . . . 100 mm
Distanza Pupilla d’Entrata ↔ Target . . . 2,0 m
Differenza massima delle distanze nell’inquadratura . +12/-10 cm (nota 2.4.1)
Nota 2.4.1) Queste sono le distanze minima e massima nell’inquadratura della foto. Le distanze, comprese nel segmento centrale dell’Autofocus, sono circa 2 cm.
L’obiettivo va avanti e indietro tra 0,8 m e 3 m per 7/8 volte, forse di più, impiegando 1÷1,5 secondi.
Alla fine mette a fuoco in modo abbastanza preciso sul target.
Non credo sia dovuto alle distanze multiple nel campo inquadrato, ma al battimento tra le linee regolari della scala inclinata e i pixel del sensore AF.
Altri fenomeni, forse, riconducibili al caso precedente.
Immagine A1_Q2m
Luce . . . 13 EV
Diaframma . . F/1,4
Focale . . . 50 mm
Distanza . . 0.45 m (circa)
Le dimensioni dei quadratini sono 2×2 mm che sul sensore diventano circa 0,2×0,2 mm.
Tutta l’inquadratura è sul medesimo piano.
Target e fotocamera sono in bolla.
L’obiettivo, partendo da infinito, riduce la distanza con un piccolo scatto poi oscilla avanti e indietro sulla nuova posizione per numerose volte. Altro piccolo scatto e altra oscillazione.
Dopo alcune volte arriva al punto di messa a fuoco e si ferma. In tutto impiega dai 10 ai 15 secondi.
La messa a fuoco è abbastanza precisa. Il confronto con l’immagine di riferimento (A8) e con i quadratini di dimensioni doppie ( A1_Q4m = 4 mm).
Raddoppiando la distanza (1,0 m) il comportamento atipico accade con i quadratini di dimensione doppia (A1_Q4m = 4 mm) che, sul sensore, hanno circa le medesime dimensioni di quelli precedenti da 2 mm.
Il comportamento qui è ancora più strano. Partendo da infinito fa il primo piccolo scatto e poi continua a oscillare attorno alla posizione senza mai smettere. Io l’ho spento dopo tre minuti.
Dimensioni effettive dei quadratini sul piano focale.
La scala lineare di 20 cm sul target ci dà la traduzione (mm del soggetto) → (Pixel del sensore).
Un pixel della 5D mk0 è 8,2 μm, quello del sensore AF non lo so.
Nell’immagine precedente 20 cm = 2657 pixel; 2 mm = 26,57 pixel = 210 um.
In questa 20 cm = 1163 pixel: 4 mm = 23,26 pixel = 191 um.
Con array ripetitivi, e paralleli al sensore, attorno ai 200 um (sul piano focale) succede qualcosa di brutto.
Credo che questo sia dovuto al battimento, o effetto moiré, tra l’array di pixel del sensore AF e l’array di righe del target. Si veda anche il capitolo 6.4.
Se questa spiegazione è vera (non lo so, per ora è una mia ipotesi) non si dovrebbe mai verificare con i soggetti naturali poiché non presentano (quasi)mai array regolari.
Secondo caso particolare.
Immagini A1_Q1m_45, A1_Q2m_45, A1_Q4m_45 (figura 2.4.3 a sinistra).
Luce . . . 12 EV
Diaframma . . F/1,4
Focale . . . 50 mm
Distanza . . 1,0 m (circa)
Le dimensioni dei quadratini, orientati a 45°, sono 4×4 mm, 2×2 mm e 1×1 mm.
Tutta l’inquadratura è sul medesimo piano. Target e fotocamera sono in bolla.
L’obiettivo, partendo da infinito, non esegue il minimo movimento.
Forse ho imbroccato i 45° esatti per cui il sensore AF non vede nessuna linea né orizzontale né verticale e, per lui è come se si trattasse di una parete perfettamente uniforme. Estremamente improbabile ma non impossibile.
Con l’immagine A1_Q05m_45 (quadratini di 0,5 mm) mette a fuoco, ma penso si tratti di effetto moiré.
Non so sul sensore AF, ma sul sensore d’immagine l’effetto è visibile molto chiaramente.